MERCI

 

Visiteurs d’un jour

Ou amis de toujours,

Connaissances réelles

Ou juste virtuelles

Qui venez regarder,

Piocher, récupérer,

Des projets , des idées,

Sur mon blog adoré,

Par accident 

ou régulièrement.

 

En ce jour particulier

Du million dépassé,

Quelques mots pour vous dire

Et surtout vous l’écrire

Notre métier est aventure

Il peut souvent être dur!

Que de défis à relever!

Que d’élèves à intéresser!

Que de montagnes à soulever!

Que d’énergie à dépenser!

Pour pouvoir bien enseigner

Il faut garder le feu sacré.

Quelle chance que le partage

Pour se redonner du courage

Rien de mieux que d ’échanger

 

Pour se sentir renouvelé.

 

 

Merci d’être à mes côtés

Tout aussi passionnés

Physiquement  

ou virtuellement 

C’est vous qui me donnez

Depuis le commencement

Et ce, pour très longtemps

Cette envie de créer

et de me dépasser,

 

Cette force incroyable

Vous êtes formidables!

 

 

MERCI! MERCI! MERCI!

Pour vous tous aujourd’hui

 

 

 

Ombeleen de Petite Luciole

 

Cela fait plusieurs années que je travaille le genre policier en classe. Au fil des années, j'ai créé puis amélioré mes propres outils qui fonctionnent  très bien. 

Si vous souhaitez voir mes anciennes séances c'est ICI

 

  ----------------------------

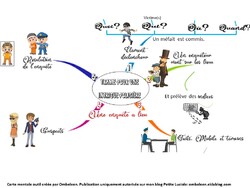
JE RECONNAIS LE GENRE POLICIER: Les élèves doivent comprendre la spécificité de ce genre de texte narratif. Pour cela, des romans policiers dont ceux que nous allons étudier, sont mélangés avec d'autres genres. Ils doivent me dire si c'est un  roman policier et pourquoi . Petit à petit, le vocabulaire émerge ...

 Question: qu'est-ce qu'il faut dans un livre pour que ce soit un roman policier?

 ---------------------------- 

1) JE LIS DES ROMANS POLICIERS

Pour que mes élèves se familiarisent avec ce genre, il est essentiel de leur proposer au préalable une séquence de lecture sur un roman policier.

 

-----------------------------

Cette année, j'ai découvert, dans ma classe, en 30 exemplaires,  le mini roman policier: Menaces dans la nuit de Marc Villard.

Etudier ce livre  a plusieurs avantages:

- d'abord il est court: une quarantaine de pages;

- même si la fin m'a un peu déroutée au début (car il s'agit d'une fin ouverte, c'est à dire qu'on a des doutes sur le coupable) j'ai compris ensuite que c'était parfait pour  faire imaginer une fin aux élèves qui seront certainement aussi frustrés que moi.  J'ai d'ailleurs prévu moi-même une fin en surprise, une fois qu'ils m'auront lu la leur (à la fin du diaporama). J'ai volontairement utilisé la narration   à la 1ère personne du singulier, contrairement à l'auteur . 

Et voici aussi les questionnaires du livre que j'ai créés pour l'occasion. (2 niveaux+ 1 corrigé)

Télécharger « Corr Lecture mini roman policier.pdf »

 ----------------------------

Je vous conseille également l'assassin  habite à côté

Exploitation pédagogique de l'assassin qui habite à côté  ICI ou LA

 ---------------------------- 

Un tueur à ma porte est très bien aussi mais plus pour des CM2/6ème . 

 Lien exploitation pédagogique d'un tueur à ma porte ICI

 ----------------------------

Vous avez aussi un rallye lecture avec les ouvrages  ICI

avec les questionnaires par niveau  ici

----------------------------

----------------------------

Pour chaque ouvrage,  nous avons complété la trame narrative vierge suivante. 

 ----------------------------

 ----------------------------

2) J'APPRENDS ETAPE PAR ETAPE A ECRIRE UNE INTRIGUE POLICIERE

Voici la trame narrative complétée,  construite avec eux après avoir lu des romans policiers.

Et voici les cartes étapes d'écriture prévues pour cette séquence.

 

Démo vidéo de la carte interactive ci-dessus

 

 

Et voici quelques outils pour les différentes étapes.

Télécharger « Etape 1 le méfait.pdf »

Télécharger « étape 2 portrait des personnages.pdf »

Pour travailler la recherche du coupable

Télécharger « L'histoire dont vous êtes l'enquêteur.pdf »

J'ai repris et amélioré l'intrigue à la manière d'Agatha Christie que nous avions créée, il y a plus de 10 ans avec des élèves de CE2-CM1. Ce qui est fou, c'est que récemment, j'ai recroisé une de mes élèves maintenant étudiante, qui me disait combien ce projet l'avait marquée, elle s'en souvenait même très bien. 

PETIT +: Il est possible de théâtraliser les interrogatoires du diaporama: Histoire dont vous êtes l'enquêteur pour permettre une vision plus réelle de la situation. Cela permettrait aux élèves qui le souhaitent de travailler leur mise en voix . 

Voici un lien pour les enquêtes de l'inspecteur Lafouine ICI

 

Si vous avez besoin de revoir le portrait, je l'ai travaillé à plusieurs reprises, pour le plus récent voir période 2 de cet article ICI

Et voici quelques supports élèves pour l'écriture de l'intrigue policière.

 

 

Bonne séquence de votre classe!

 

N'hésitez pas à me dire si vous voyez des coquilles qui m'auraient échappé ... Merci!

 

Cela fait un moment que je voulais vous partager cette séance d'art visuel qui restera un moment fort pour les élèves de ma classe. Je profite donc des vacances pour le faire. 

VAN GOGH

Nous avons art visuel le vendredi après-midi, du coup, pour  mettre mes élèves en appétit, nous avons observé en rituel d'histoire des arts visuels, chaque matin, une œuvre de Van Gogh, dont le ciel étoilé bien entendu. 

Je leur ai fait visionner 2 vidéos pour les familiariser avec la façon de peindre de l'artiste. 

Petite vidéo sur un autre ciel étoilé de Van Gogh ICI

Explication de l'oeuvre de Van Gogh

 

 

Attention la peinture acrylique tache, nous avions donc prévu de vieux vêtements ou tabliers de peinture.

Je leur ai présenté les étapes pour parvenir à l'oeuvre finale. 

 

 

 

 

 

 

 

 

Comme vous pouvez le voir, il n'y a que deux bleus. Ce sont eux qui par des mélanges, devaient créer les autres.

 

 

 

 

 

 

 

 

Certains ne savaient pas faire du vert. Ils ont donc tenté des mélanges pour en obtenir. 

 

 

 

 

 

La séance 4 a duré plus longtemps que prévu (+ 1 séance) car certains élèves ont voulu retravailler certaines couches de peinture. 

 

Mes élèves ont beaucoup aimé manipuler la peinture. Ils me le réclament encore. Même si le lavage et le nettoyage sont un peu longs, je ne regrette pas du tout cette séquence qui leur a beaucoup plu.  Chaque œuvre a sa particularité et franchement je suis très fière du résultat qui est encore mieux que sur les photos car on voit plus clairement les couches de peinture.

 

 

Quel bonheur d'avoir une classe comme la mienne!

J'aime voir mes élèves avec des étoiles plein les yeux... heureux d'apprendre! 

 

Je ne résiste pas à l'envie de vous partager mes dernières traces écrites essentiellement des cartes mentales qui ont pour but une réactivation plus rapide et plus visuelle de la leçon. Je n'ai pas de logiciel particulier à part power point , je mets un fond transparent avec photo filtre, ce qui me permet d'assembler toutes les images que je veux. Je crée ensuite des zones de textes en utilisant la police d'écriture qui me semble la plus adaptée.

Ces traces écrites sont systématiquement amenées par des situations de recherche. Une fois leurs recherches terminées, la leçon n'est plus qu'une formalité puisqu'ils ont tout trouvé  par eux-mêmes, nous passons alors à la mise en mots de ce qu'ils ont appris (phase d'oralisation) puis à la carte mentale (organisation spatiale)  qui servira à réactiver ce qu'ils ont mémorisé à ce moment-là.

Je rappelle que je m'appuie sur tout ce que j'ai pu lire dans les ouvrages actuels traitant des dernières avancées en neurosciences concernant la mémoire. Par exemple, pour mémoriser les verbes d'état, je leur ai mis des images évoquant le premier phonème de chaque verbe, ces indices de récupération leur permettent de mémoriser plus facilement et de façon plus concrète, ces verbes.

 

 

 

 

 

   

Traces écrites français           

 

 --------------------------------------

Ma nouvelle méthode d'orthographe

J'utilise la fabuleuse méthode de Retz:

Réussir en orthographe en CM1.

 

Je tiens à vous la présenter aujourd'hui car je trouve qu'elle permet aux élèves sur le long terme d'avoir un bon niveau en orthographe en les aidant à acquérir des réflexes quotidiens. 

Elle se fonde sur 2 bases de données MANULEX (pour connaitre la fréquence d'un mot) et EOLE (échelle d'acquisition des 12 000 mots les plus fréquents classés du CP au CM2). Les mots étudiés sont donc soigneusement choisis pour correspondre aux plus fréquents et aux plus accessibles d'une tranche d'âge donnée.

Voici un exemple de rituels quotidiens pour la séquence 1 

 

Les séquences sont progressives et commencent par les mots invariables plus simples à mémoriser puisqu'ils ne changent pas.

Unité 1: les relations oral /écrit

- Alphabet Phonétique international

- Comment bien écrire les mots invariables?

- Comment bien écrire les lettres finales muettes?

- Comment bien écrire le son [s]?

- Quel son peut faire  la lettre g ?

Des listes sont à apprendre progressivement. Une leçon d'orthographe est prévue par semaine pour établir après  recherches, les règles qui régissent l'orthographe. 

 

 

 

 

Une dictée bilan est prévu chaque semaine (3 niveaux prévus)

 

Voici les 2 cartes mentales que j'ai créées en complément de la méthode .

Unité 2: Les marques orales et écrites- les pluriels.

- Chaines d'accord en nombre dans le GN et la phrase.

- Les pluriels réguliers et irréguliers des noms et des adjectifs 

Pour le moment, j'en suis là et je vois les progrès quotidiens de mes élèves grâce à cette méthode qui est vraiment  très bien pensée et ludique.

Exemple de dictées quotidiennes puis hebdomadaire séquence 2

 

 

Il nous reste:

Unité 3: Les accords en nombre et en genre

Exemple de  dictée hebdomadaire pour la séquence 3

Unité 4:  Les relations entre l'oral et l'écrit

- adverbe en -ment

- Comment écrire le sont [j] en fin de mots?

- Comment bien écrire les mots féminins terminés par [te] etc.

Exemple de dictée hebdomadaire pour la séquence 4

Gros plus: 

Il y a beaucoup de propositions pédagogiques très intéressantes dans cette méthode mais il serait facile d'être un peu perdu sans l'ouvrage papier qui accompagne les fiches du CD ROM (de nombreuses fiches d'entrainement). Il  permet  d'avoir une vue globale et précise de chaque séquence. De plus l'ouvrage est très récent ( octobre 2019) il tient compte des dernières recommandations du ministère de l'éducation nationale.

 

Voici le lien vers l'ouvrage, en espérant vous avoir donné envie...

 

 

 

                                                      

Je suis extrêmement fière de mes élèves et du travail titanesque qu'on a fourni durant cette année pour que ce projet puisse aboutir. 

Franchement c'est le projet le plus riche que j'ai eu à mener durant toutes ces années. Je me suis même découvert des talents cachés. D'ailleurs si vous souhaitez travailler la rédaction en lien avec l'environnement et les légendes avec un rendu  artistique, je vous le conseille vraiment.

C'est un projet amateur et il y a certainement des imperfections dans l'enregistrement puisque je ne suis pas ingénieur du son mais ce n'est pas cela l'important. Avec les élèves on a écrit des textes, ils y ont pris du plaisir et ont découvert le métier d'auteur de A à Z. Ils ont développé tout un univers imaginaire et chacun y a participé avec ses talents...  Je comprends que certains auteurs viennent s'inspirer dans les classes. J'ai été impressionnée par les milliards d'idées que le groupe classe a pu avoir. La mise en voix a été aussi une découverte pour ce groupe classe, pas très à l'aise, avec l'oral (d'où le choix du projet). Au départ timides et mal à l'aise, ils m'ont impressionnée par leur  aisance au fil des prises. Pour certains, cela a même été une véritable révélation… 

Ce CD s'est donc fait dans la joie et la bonne humeur avec une certaine exigence de leur part (Ils savaient très bien s'ils avaient réussi ou non leur mise en voix et demandaient spontanément à la refaire si ce n'était pas bon) et je pense que pour eux comme pour moi, cela restera un merveilleux souvenir… Même l'ambiance dans la classe a changé au fil du projet; ils se sont découverts les uns les autres et  sont plus soudés et plus solidaires qu'avant. 

Je vous laisse découvrir par vous même en cliquant sur l'image

 

Quel défi pour nous que de transformer notre pratique pour faire  classe à distance! Il est très important que les élèves puissent ne pas prendre trop de retard dans les apprentissages fondamentaux.

Je suis actuellement en pleine préparation de travail pour ma classe de Moyenne Section.

Voici une chanson sur l'alphabet qui je l'espère motivera mes élèves...

 

Il est essentiel et j'espère que les parents l'ont compris, qu'ils travaillent la motricité fine tous les jours. J'ai donc préparé de petits tutoriels de pâte à modeler. 

JOUR 1: l'arbre

 

JOUR 2: la fleur

JOUR 3 : le tableau en pâte à modeler

JOUR 4: La grenouille

 

Télécharger « Travail en graphisme blog.pdf »

 

Compréhension en lecture

J'utilise en compréhension, la méthode Narramus que l'inspecteur m'a conseillée lors de mon rendez-vous de carrière et elle est vraiment très  bien. Merci à lui!

 

Durant cette période, je travaille sur l'album Petite Taupe ouvre-moi ta porte.

Voici un  diaporama qui est complémentaire à cette méthode sur l'ouvrage Petite Taupe, Ouvre-moi ta porte

Télécharger « Documents complémentaires méthode Narramus  blog.pdf »

Je peux également vous partager la bande son qui raconte l'histoire jusque là où nous en sommes  puisqu'il s'agit d'une création personnelle pour aider mes élèves, la bande son du DVD n'étant pas top au niveau de la qualité du son.

module 3: jusqu'au blaireau

module 4: jusqu'à la mésange

 module 5: jusqu'au loup

module 6: complément à la méthode pour aider à la mémorisation de l'ordre des personnages.

Télécharger « Complément méthode Narramus module 6.pdf »

 

Cette méthode est vraiment géniale, elle fait travailler le vocabulaire, la compréhension, la reformulation, la fabrication d'un livre et permet aux enfants d'apprendre à comprendre en développant leur capacité à raconter.

 Voici quelques images pour avoir un aperçu:

 

Images pour travailler le vocabulaire

 

 Dictée à l'adulte de ce que dit le blaireau.

 

Exemple de masques

 Des photos à venir...

 

Cette méthode se sert des avancées en neuro sciences pour les aider à mémoriser. Je suis très enthousiasme car elle est complète, clé en main , il y a même les marionnettes pour jouer l'histoire et concerne selon les albums, les PS-MS-GS et CP. Un album est fourni avec . En voici quelques exemples, vous pouvez cliquer sur les images ci-dessous

 A très vite...

Bonjour à tous,

Cela fait longtemps que je n'ai pas écrit d'articles car j'avais besoin de me plonger dans mon nouveau niveau et mon nouvel établissement. Je sais que le blog est majoritairement lu par des enseignants de cycle 3 mais j'ai préparé un article sur la maternelle que je souhaite vous partager. Ce changement m'a fait voir certaines choses sous un autre angle et  le jour où je retournerai en cycle 3, je n'enseignerai pas tout à fait de la même façon.

Ce qui est génial en maternelle c'est que les enfants sont partants pour tout, sont curieux de tout et que l'enseignant les éveille à une foule de choses, je vois déjà une évolution en un mois et demi de classe.  Cette envie, ce besoin de grandir et d'apprendre est alimenté par une multitude d'activités ludiques et motivantes: l'enfant bouge, apprend à son rythme, et il est confiant en ce qu'il peut faire.

Cette motivation et cet enthousiasme diminuent chez beaucoup trop d'élèves, je trouve, au cours de la scolarité: classes trop statiques (et pour cause un manque de place et de moyens bien souvent), savoirs cloisonnés, pression du résultat et des parents , jeux vidéos à outrance et j'en passe… Quel dommage!

Le truc, c'est que la motivation est tellement importante, on apprend tellement mieux avec… Je m'interroge aujourd'hui sur comment cette expérience en maternelle peut enrichir ma pratique en cycle 3... et j'ai déjà quelques idées…que je mûris.  

 

Comme vous le savez, je m'intéresse de très près à l'avancée des neurosciences notamment dans le domaine de l'éducation et j'ai lu un ouvrage qui est vraiment génial. Savoir ce qui se passe dans la tête d'un enfant quand il est en colère, comprendre comment aider un enfant qui ne maitrise pas ses émotions… cet ouvrage fourmille de mille explications scientifiques avec des schémas  pour mieux comprendre et rejoindre un enfant en difficulté émotionnelle. J'ai déjà testé certaines choses et ça marche!!!

 

Pour finir, voici les documents dont je me suis servie pour ce début d'année en MS  ICI

Cela fait longtemps que je n'ai pas donné de nouvelles et pour cause cette année est l'année du changement pour moi: changement d'école,  changement de niveau et de cycle. Je passe en cycle 1, moyenne section de maternelle. Après de très nombreuses années en cycle 3, il était important que je quitte ma zone de confort … De nouveaux défis et pleins de bons moments en perspective...

Je laisse à votre disposition, toutes les ressources CE2, CM1 et CM2 du blog et si vous avez des questions, n'hésitez pas.

Belle visite à vous. A très vite!

L'un de vous m'a signalé qu'il n'avait pas accès au dernier article car un mot de passe le protégeait. Je suis allée voir et effectivement mon article s'était mis par défaut dans une rubrique protégée. C'est réglé! Vous pouvez le lire ICI. Bonne lecture et belle journée à vous!!

 

Voici le lien vers la rubrique géographie que je viens d'étoffer:

La nature en ville en géographie ICI

 

Bonne lecture! 

Travailler la poésie n'est pas simple. Pourtant, jouer avec la langue et les émotions est un moyen d'expression tout à fait extraordinaire!

Je vous partage aujourd'hui la séquence réalisée en classe  et qui a donné naissance à de très jolies productions! Je suis vraiment fière d'avoir pu  accompagner mes élèves dans cette découverte.

Une chanson est même née à partir de leur dernier poème. 

Je vous invite donc à découvrir cette séquence  en cliquant sur le lien ICI

 

Si cela vous inspire, n'hésitez pas à me laisser un petit commentaire… Merci!

 

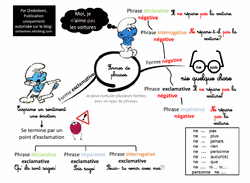
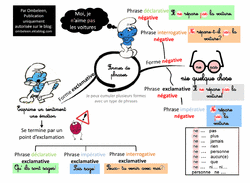
Cet été en me penchant sur les programmes, je me suis aperçue que la phrase exclamative avait basculé dans les formes de phrases et plus dans les types de phrase.

 

Une ancienne collègue avec un DEUG de lettres m'avait parlé de cette erreur, il y a quelques années,  sur la phrase exclamative qui n'était pas, en fait, un type de phrase mais comme c'était dans les programmes, je continuais de l'enseigner comme ça. 

En creusant, j'ai trouvé une explication très claire de madame Picot sur  pourquoi il s'agit d'une forme et pas d'un type de phrases,  dans les commentaires ICI

Du coup  pendant les vacances, j'ai cogité pour savoir comment désapprendre aux élèves ce concept pour le réapprendre correctement.

Je vous partage ici le diaporama sur ces 3 séances: une sur les types de phrases, une sur la forme négative, une sur la forme exclamative.

 J'ai mis un test rapide à la fin de chaque nouvelle séance car, selon les neurosciences, il s'agit du meilleur moyen pour l'élève de vérifier s'il sait et de pouvoir y remédier s'il se rend compte qu'il ne sait pas. De plus cela renforce la mémorisation à long terme d'après les dernières expériences scientifiques. Du coup, j'expérimente...

Télécharger « types et formes de phrase.pdf »

Et voici deux cartes mentales qui sont présentes aussi dans le diaporama.

 

Erratum: version modifiée

Télécharger « formes de phrases.pdf »

 

Attention, à la négation dans une phrase interrogative :

ex: Ne mange-t-il pas à la cantine? Si pour une affirmation qui contredit la négation de la question . Non s'il ne mange pas.

 

Si cela vous a plu ou aidé, n'hésitez pas à laisser un commentaire!

Voici un nouvel article que j'ai écrit pour Beneylu ICI

 

Suite aux messages de certaines d entre vous me demandant le mot de passe pour les lecons interactives, j' ai enfin compris pourquoi on vous demandait un mot de passe que je n' avais pas mis. L  article était associé à la partie privée du blog, qui elle , a un mot de passe. J ai normalement rectifié...N  hésitez pas à me recontacter si le problème persiste. 

Bonne journée à vous! Et bonne visite sur le blog!

Je remets un lien vers cette rubrique car j'y ai ajouté des cartes mentales....ICI

Bonne visite

 

 Vous avez dû apercevoir de drôles de personnages dans mes cartes mentales de grammaire...

 

En effet, cette année, j'ai décidé de fabriquer mes propres personnages de grammaire (inspirés par les Monsieur-Madame et de Retz ) pour aider mes élèves dans leurs analyses grammaticales. La grammaire  est parfois si abstraite pour certains... Cela permet aux élèves, en rituel, le matin, de parvenir à les reconnaître dans une phrase. 

 

 Ces personnages ont des indices de reconnaissance permettant de visualiser plus facilement chaque  nature.

 

Voici une petite explication  des personnages particuliers:

L'adverbe tient le verbe, l'adjectif et un autre adverbe à l'envers car il peut modifier le sens de ces classes grammaticales. (change le sens= visuel à l'envers)

Il mange peu

Il travaille  très vite

Il est trop triste

--------------------------------------------------

Le pronom a les bras longs qui tiennent un nom car il  remplace un nom ou un GN.

----------------------------------------------

Le verbe: avec un marteau d'un côté= verbe d'action avec des smileys de l'autre= verbe d'état (introduit un état) .

----------------------------------------

Conjonction: lie 2 idées.

---------------------------------------

La préposition: elle introduit un complément.

-------------------------------------------------

Le nom: il a un mégaphone car il  nomme les objets, animaux, choses, idées... Il peut désigner en général= nom commun ou en particulier= nom propre.

-----------------------------------------------

Le déterminant: permet de connaître le genre et le nombre (personnages entre ses mains).

----------------------------------------------------

L'adjectif qualificatif: permet de donner des précisions au nom: chapeau pointu, rond, vert, étoilé, marron etc...  

 

Voici ces personnages regroupés en une seule feuille en couleur ou à colorier. 

Télécharger « personnages grammaire regroupement2.pdf »

 

Voici les wagons  des fonctions,  idée prise sur  le blog de Loustic ICI

Télécharger « wagons fonction.pdf »

Télécharger « wagons grammaire.jpg »

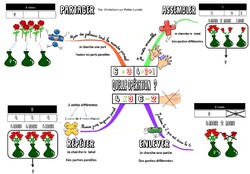
Nous avons travaillé les 4 opérations progressivement durant 2 périodes. il ne nous en manque plus qu'une: la division. 

Voici une approche qui permet de visualiser la division parmi les 3 autres opérations. Les nombres sont volontairement petits. pour permettre une manipulation et une meilleure visualisation.

 SEQUENCE 1: 

Etape 1: cherche avec le diaporama

Les élèves sont munis de leur ardoise et pour chaque étape, ils cherchent avant de visualiser la réponse.

Télécharger « les 4 opérations diaporama.pdf »

 

 

Etape 2: carte mentale

Nous en arrivons ainsi à la carte mentale suivante

Télécharger « carte mentale choisir une opération news.pdf »

 

Etape 3: entrainement seul, à deux puis en collectif

Fiche d'exercices:

recherches seuls

débats à deux

débat en collectif

Les problèmes soulignés sont plus complexes.

Télécharger « 4 opérations Quelle opération pour quel problème 3.pdf »

 

L'objectif c'est d'acquérir des réflexes dans la résolution de problèmes.

Si je cherche un tout: 2 opérations possibles multiplication-addition. Pour savoir laquelle convient les parts sont égales= multiplication/ les parts sont inégales= addition.

Si je cherche une part: 2 opérations possibles= division ou soustraction. Si les parts sont égales = divisions/ si elles sont inégales= soustractions.

 

------------------------------------------------------

Après avoir vu les problèmes de division ICI

-----------------------------------------------------

SEQUENCE 3:

Diaporama: 

Télécharger « Révision sur les 4 opérations problèmes.pdf »

fiche individuelle : problèmes 4 opérations.pdf 

 

Et les voilà prêts pour l'évaluation!!!!

Il est très compliqué de faire changer certains habitus d'élèves surtout en orthographe. Cette année, j'ai décidé de travailler l'orthographe un peu différemment. 

Au début (dictées n°0, n°1, n°2) j'ai essayé de partir d'écrits de la classe mais  c'était trop long ...et pas vraiment efficace pour eux.

Depuis, j'essaie un nouveau procédé qui se révèle beaucoup plus fructueux (gros progrès entre la première dictée et la deuxième).  Cela fonctionne sur 2 semaines:

La première semaine, on travaille sur un point particulier d'orthographe. Actuellement je suis sur des sons . Le lundi, on cherche les différentes façons d'obtenir ce son puis  mardi et jeudi une liste de mots  est trouvée et mémorisée, le vendredi pour la première dictée, seuls les mots appris comptent.

La semaine suivante, j'ai souligné leurs erreurs , ils les corrigent, demandent une explication s'ils ne comprennent pas. Puis on transforme cette dictée en changeant la personne qui raconte (je, tu , il, ils...) et ils doivent la recopier en rituel en faisant les changements (les accords, les possessifs) . On corrige. Le vendredi, la dictée est à une personne différente et  porte sur tous les mots de la dictée. Comme ils les ont vus plusieurs fois, j'ai de bien meilleurs résultats.

Télécharger « les dictées période 1 et début 2.pdf »

 Télécharger « dictée n°4.pdf »

Je fais des cartes sons inspirées de mes clés de sons ICI. Je travaillerai de la même façon pour les homophones .

Si cela vous intéresse, j'en ai préparé d'autres que je mettrai au fur et à mesure.

 

Vous cherchez un fichier pour enseigner l'Histoire en cm1 clé en main avec :

1) les séquences pédagogiques sur l'intégralité des nouveaux programmes.

2) les cartes, images, vidéos à projeter

3) les situations de découvertes, des exercices interactifs + les organigrammes + frises+ biographies des personnages

4) des fiches élèves à photocopier, la trace écrite qui en découle...les évaluations, ...

 

 

En plus du support classeur  avec fiches pédagogiques et fiches élèves, il y a un DVD avec tout ce qu'il faut pour faire une séance d'Histoire ludique, intéressante, interactive.

 Voici un exemple avec le chapitre Celtes, Gaulois, Grecs, Romains, quels héritages des mondes anciens?

 Comme vous pouvez le voir sur l'image, en plus du contenu de la séance (situation de découverte, leçon animée, qcm, trace écrite) , l'enseignant peut à tout moment consulter :

-la bibliothèque d'images pour trouver cartes et documents 

-la biographie des personnages historiques dont il est question.

 

-un organigramme qui résume et synthétise à la manière d'une carte mentale les point essentiels de la séquence.

-les frises du temps pour bien se repérer dans chaque période.

 

Et j'en passe.....

Tout est fait!

Quel gain de temps dans la préparation de mes séquences! Et la partie vidéo de  chaque leçon est vraiment bien construite! Je suis conquise!!!!!!!!

C'est pourquoi je vous le partage aujourd'hui et l'utiliserai en classe dès la semaine prochaine pour en faire profiter mes petits élèves.

 

Félicitations à Loustic pour son superbe travail!

 

Jusqu'au 30 septembre, il y a une remise, si vous êtes intéressés, c'est ICI

 

Et voilà!

Cela faisait longtemps que j'en rêvais!

Le blog a fait peau neuve! En espérant que cela vous plaira...

Bonne visite à vous!