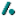-
Pratiquant la carte mentale depuis quelques années, je l'améliore au fil du temps pour qu'elle soit un outil efficace de "réactivation" de ce qui a été vu en classe.
Au début, je faisais construire la carte mentale de A à Z et elle n'était pas très présentable. J'ai donc décidé de faire différemment.
LORSQUE JE PRÉPARE MA SÉANCE
1) Je pointe les domaines clés à aborder avec les élèves .
Exemple: Pour convertir des mesures (avec une virgule).
Voici les points importants :
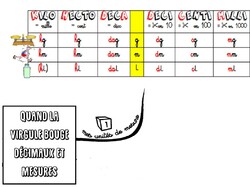
- Pour les mesures, la virgule bouge contrairement aux nombres décimaux (où elle restait entre les unités et les dixièmes).
- étape 1: il faut bien connaitre l'ordre de ses unités de mesures.
-étape 2: le chiffre juste avant la virgule correspond à l'unité .
-étape 3: je peux alors déduire la valeur de tous les autres chiffres
-étape 4: je regarde l'unité qu'on me demande et je déplace la virgule après le chiffre qui correspond à cette unité.
2) Je réfléchis à une situation de recherche avec des questions précises qui reprend point par point ces domaines à trouver.
3) Je les mets sous la forme d'une carte mentale qui sera à compléter par les élèves.
LORS DE LA SÉANCE EN CLASSE AVEC LES ÉLÈVES
4) Les élèves cherchent, confrontent leurs idées puis émergent les domaines clés qu'ils trouvent.
Exemple : Leur donner une mesure à convertir 12 cm en mm. Voir que 12cm= 12,0 cm. Que s'est -il passé avec la virgule? Où s'était-elle déplacée? (120 mm = 120,0 mm) . Quel chiffre représente l'unité ? où est-il placé par rapport à la virgule? Juste avant. Nous faisons les lunettes entre le chiffre qui représente l'unité et l'unité. Maintenant un autre: 1,25 m (la virgule est mise volontairement entre l'unité de référence le mètre et les dixièmes, centièmes de mètre pour que ce soit plus simple au début) et leur demander de la convertir en décimètre. Quels chiffres pour quelles unités? Ils comprennent assez vite que le 1= le mètre le 2 =dm et le 5= cm. Je ne veux plus des mètres mais des décimètres. Ils se rappellent ce qu'on a vu juste avant : que le chiffre avant la virgule correspond à l'unité donc si l'unité change= la virgule bouge. Où? entre les décimètres et les centimètres.
On essaie avec une autre mesure 25,104 dag à convertir en dg.
Interroger les élèves sur les étapes qu'ils ont suivies pour parvenir à convertir
5) Compléter la carte mentale n'est qu'une formalité puisqu'ils ont trouvé toutes les étapes pour parvenir à convertir une mesure lorsqu'il y a une virgule.
Ils mémorisent ensuite la carte mentale en utilisant les 3 entrées visuelle, auditive et kinesthésique.
Télécharger « quand la virgule bouge light.pdf »
6) Ils repartent chez eux avec les cartes mentales qu'ils sont capables de décoder puisque déjà mémorisées. Certains élèves préfèrent apprendre directement sur le blog classe avec la carte mentale complétée à l'ordinateur.
Pourtant quelques élèves en déficit de mémoire ne parviennent pas à se souvenir, le soir de ce que nous avons fait et dont la carte mentale n'est que le produit fini.
C'est pour eux que m'est venu l'idée de ces capsules vidéo qui racontent la carte mentale...Un peu comme si la maitresse s'invitait à la maison pour rappeler ce qui a été dit!
Pour voir d'autres capsules vidéo, c'est ICI
 2 commentaires
2 commentaires
-
Nous avons commencé notre cycle sur le policier.
1) Lecture de romans policiers
Avec le professeur de français de 6ème (décloisonnement) les élèves ont lu et étudié un tueur à ma porte.
------------------------------------------
2) début d'intrigue policière
Puis ils ont essayé d'écrire le début d'une intrigue policière à la manière de...
Télécharger « début d'une intrigue policière.pdf »
---------------------------------------------------
3) L'affaire du manoir (prévoir 1h30)
Armés d'un stylo et de la feuille des suspects, les élèves se sont métamorphosés, le temps d'une séance en véritables détectives et ils ont tenté de résoudre l'affaire du manoir, intrigue policière écrite par mes élèves, il y a quelques années.
fiche élève notes et portraits des suspects affaire du manoir.pdf »
Affaire du manoir portraits et interrogatoires suspects
Le débat sur la résolution de cette affaire a été long et intense. Certains avaient l'un des deux coupables, d'autres le bon nombre mais personne n'avait trouvé l'intégralité de l'intrigue. Néanmoins, ils ont tous fourni une réflexion approfondie et argumentée sur le sujet. Très bonne séance!
Et vous? Avez-vous trouvé?
Télécharger « Résolution de l.pdf »
-------------------------------------------------------
La suite de la séquence à suivre....
 1 commentaire
1 commentaire
-
En lien avec mon projet d'année H2O, nous avons vu le texte poétique. Je vous partage ma progression et leurs réalisations.
séance 1: découverte du calligramme
C'est ainsi que Guillaume Apollinaire a intitulé l'un de ses recueils de poésie, paru en 1918. C'est aussi une façon amusante d'écrire un texte en lui donnant la forme d'un dessin. Entre Calligraphie et Idéogramme, ce mot valise, inventé par Apollinaire lui-même, est à lui seul la promesse d'un jeu sur les mots. Voici quelques exemples de calligrammes. Prévoir des calligrammes vidéoprojetés. Les élèves font leurs observations.
Télécharger « séance 1 les calligrammes fiche élève.pdf »
------------------------------------------------------
séance 2: comment est construit un poème?
Avant de faire le dessin, il faut créer le texte. Nous allons donc voir comment se construit un poème en prose. Poésie signifie créer. La poésie a le pouvoir de créer par des mots, une émotion, un sentiment chez l’auditeur ou le lecteur.
Comment construit-on un poème ? Voici un poème en vers. (fiche élève 2)
Télécharger « fiche élève 2 comment se construit un poème.pdf »
Télécharger « fiche élève 2 correction.jpg »
La poésie est souvent écrite en vers .
Qu’est-ce que c’est ? Le vers commence par une majuscule même si ce n’est pas le début de la phrase. = ligne de la poésie.
Combien ce texte a-t-il de vers ? a 12 vers.
Chaque vers a un nombre de pieds. Qu’est-ce que c’est ?
Ce sont les syllabes que l’on doit prononcer. Le faire avec les mains pour vérifier. Relire la poésie en comptant le nombre de pieds en tapant dans les mains.
Combien de pieds dans ce poème ?a 7 pieds par vers (c’est régulier comme un rythme). Souvent les vers se terminent par des rimes. Prendre des crayons de couleurs et colorier la finale des vers de la même couleur lorsqu’elle se termine pareille. = une rime.
e le faire au tableau. La rime est une répétition à la fin d’un vers de la dernière syllabe. Un poème en vers a une forme particulière.
Les vers composent des strophes ABBA ou ABAB (leur montrer à quoi cela correspond).
Voir avec le poème. La strophe est un ensemble de vers correspondant à un système de rime complet.
Combien de strophes ici ? 5 strophes.
Sens de la poésie qu'est-ce qu'un anagramme? autre mot avec les mêmes lettres mais dans un ordre différent. neige= génie / neige= génie / chien= niche etc.
-----------------------------------------------------
séance 3: jouer avec la langue en créant des rimes qui ont du sens.
Exercice 1: classe entière.
Prendre des noms de villes à la rime facile et trouver des rimes sur la météo en i, en eil, en eux, en an et en el. EX: Paris/ Marseille / Montreux/ Royan/ La Rochelle/ Rouen
Faire une liste météo: Pluie / soleil/ nuageux ou pluvieux/ vent/ grèle/ beau temps
Il faut maintenant les mettre en phrase. Voilà ce que cela a donné pour la classe
Pour Paris, de la pluie
Pour Marseille du soleil
Pour Montreux, nuageux
Pour Royan, mauvais temps,
Pour la Rochelle, de la grêle
Pour Rouen, très beau temps
Il ne manque plus que la fin: lien entre ce que ressent la personne et la météo = conclusion sentiments
Et dans mon coeur , du Bonheur
-------------------
Exemple 2 : prénoms et fleurs
Prendre des prénoms à la rime facile en: Carole, Anaïs, Léa, Margaux, Adrien, Lily ...
Réfléchir à des fleurs qui riment avec: tournesol, iris, bégonia, coquelicot, romarin, pissenlit,...
Ce que la classe a trouvé:
Pour Carole, du tournesol,
Pour Anaïs, un iris,
Pour Léa un bégonia
Pour Margaux, un coquelicot,
Pour Adrien, du romarin,
Pour Lily, du pissenlit
Maintenant, il faut une fin pour conclure le poème, en lien avec les fleurs et les sentiments, les élèves ont trouvé plusieurs fins , voici ma préférée:
Mais pour toi, une fleur ne suffirait pas,
Je t’offrirai, moi, un bouquet de dahlias
Possibilités de poursuivre avec les aliments + prénoms
Une fois que les élèves ont compris le principe. Je les lance sur le projet d'écriture d'un poème, seul.
séance 4: écriture d'un poème individuel en plusieurs jets.
Télécharger « fiche élève 3 construire un poème sur la mer.pdf »
Réalisations
Si le sable devenait eau
Si le Saint-pierre priait avec des bigorneaux
Si la baleine avait des palmes
Mon bateau coulerait aussitôt
Si le requin savait marcher
Il m'aurait tout de suite dévoré
Si la méduse ne savait pas nager
Elle s'agripperait à une bouée
Si l'hippocampe avait des lentes
Il se frotterait contre une plante
Et si les mouettes nageaient dans la mer
Elle serait vraiment à l'envers !
Gabriel CM2
Si le bateau était sous l'eau
Les matelot ne feraient plus hissé ho
Si la mer était la terre
Le poisson chat attraperait de gros rats
Si roi Claudion était un saumon ,
Les paysans deviendraient des capelans
Si l'océan était absent,
Le corail se changerait en broussailles,
Les poissons vaudraient des millions.
Si la mer était a l'envers ,
Tout irait de travers
Stéphanie cm1
Si les mouettes nageaient dans la mer
Si les poissons volaient dans l'air
Si la mer n'avait plus d'eau
Si dans le ciel, volaient des bateaux
Si la mer était sucrée
l'eau douce serait-elle salée?
Si les abysses se trouvaient dans l'espace
Il y aurait beaucoup de place.
Si le poisson- marteau était un clou
Il serait enfoncé dans la boue
Si le poisson mangeait la mouette
la mangerait-il avec de la vinaigrette?
Notre mer serait bien ennuyeuse
A côté de cette mer joyeuse.
Pawel CM2
Si les poissons avaient des bras,
mangeraient-ils du chocolat?
Si les bateaux ne flottaient pas sur l'eau,
Leurs voiles croiseraient-elles les étoiles?
Si le crabe faisait la loi,
s'appellerait-il Baracuda?
Si les poissons avaient écrit la constitution,
les humains dans un bocal tourneraient en rond.
Si la sardine conduisait un camion,
elle ferait des queues de poisson
Si la pieuvre conduisait un chalutier,
elle finirait dans un palmier.
Tout serait à l'envers
dans cette mer imaginaire.
Benjamin CM
Si le poisson -clown ne faisait plus rigoler,
Si la raie plate était gondolée
Si le poisson-lune se transformait en soleil
Si le requin mangerait des abeilles
Si le lieu n'avait pas le sens de l'orientation
Si la baleine savait résoudre des équations
Si le brochet n'était pas carnassier
Si le narval était Congolais
Si le poisson-chat faisait miaou
Si le bar servait des vins d'Anjou
Si le pomoxis avait plein d'amis
Si la sardine était aussi rare que le rubis
Si le thon n'était plus aussi cher
Que serait le monde sur Terre?
Adrien CM2
Si dans la mer tout était à l'envers,
Si les sous-marins étaient sous-terrain
Si le poisson chirurgien était médecin
Si la terre s'appelait la mer
Si les requins clairs étaient verts
Si les poissonniers vendaient du blé
Si les poissons anges s'appelaient diables
Si l'océan Indien était européen
et si le thon était rond
Dans la mer, tout serait à l'envers.
Pierre CM2
Si la mer était à l'envers
Si les marins sur leur bateau
péchaient avec leur chef Néo.
Si leurs grands tonneaux
étaient remplis de vin nouveau.
Si les anguilles
étaient droites comme des aiguilles
La murène serait-elle jalouse?
Si l'ours était dans la mer
l'oursin serait-il sur terre?
Si le cheval allait dans l'eau
l'hippocampe serait-il sur terre?
Ce serait une mer
à l'envers
Diégo CM1
---------------------------------
Prolongement:
Ecrire un mini calligramme sur un animal marin choisi
 votre commentaire
votre commentaire
-
Ceci est la suite de la division euclidienne séance 1 ICI
Voici la 2ème séance qui traite des 2 types de divisions et qui aidera les élèves à résoudre des problèmes de division.
Voici le lien chez Beneylu Pssst de mon article ICI
Et voici les documents originels
Télécharger « article 2 les 2 types de divisions.pdf »
 4 commentaires
4 commentaires
-
Rendre l'Histoire plus vivante en attribuant le rôle d'un personnage historique aux élèves, c'est possible!
La révolution française est la conséquence d'une crise bien réelle dans la société française . La convocation des Etats-Généraux par le roi Louis XVI est la réponse du roi apportée aux mécontentements de son peuple face à la crise économique et financière que traversait son royaume. Cette convocation entraine un énorme espoir de renouveau de la part du Tiers-Etat. Mais pour qu'il y ait renouveau, il fallait pour le Tiers-Etat que sa voix compte plus que celle des 2 autres ordres....et ce n'était pas le cas!
Comment le Tiers-Etat (rejoint par des membres des 2 autres ordres) va-t-il parvenir à se faire entendre et va-t-il réformer profondément le système politique français?
Pour que les élèves puissent comprendre tout cela, ils se sont mis dans la peau de députés des 3 ordres, une théâtralisation a été proposée à la classe, suivie ensuite d'une explication de ce qui s'est passé et du rôle que chaque personnage a joué dans ce bouleversement majeur de la politique française. Ce fut un grand moment de classe!
Cette séance, je la partage sur Beneyluscool ICI
Voici la séance originelle
Télécharger « Théâtraliser les Etats généraux.pdf »
annexes:
Télécharger « Les personnages à distribuer aux enfants.pdf »
Télécharger « les célébrités des Etats généraux.pdf »
 11 commentaires
11 commentaires
-
Notre cycle sur le portrait est terminé, voici la façon dont j'ai travaillé avec ma classe pas franchement à l'aise avec cet exercice...

Avoir des idées , savoir les structurer et les mettre en phrases bien construites, reste un exercice extrêmement complexe pour les élèves; surtout lorsque beaucoup d'entre eux, n'ont qu'un intérêt très limité pour la lecture et n'ont donc pas les structures de phrases expertes en tête . Au fil des années, je me suis rendue compte que plus on donnait de modèles rédactionnels à l'élève, plus il pouvait s'améliorer et apprendre à rédiger car la rédaction est rarement innée. Voici la trame de ce que j'ai construit dans ma classe avec les élèves et qui leur a permis de progresser. Je me suis bien sûr adaptée à leurs besoins.
ETAPE 1: OBSERVATION DE PORTRAITS
Qu'est-ce qu'un portrait? Quels sont ses codes? Comment peut-on en construire un?
Pour les aider à se créer des images mentales, chaque portrait en mots a son équivalent en dessin (à finir) .
Télécharger « portrait rédaction étape 1.pdf »
ETAPE 2: LEXIQUE: CHAMP LEXICAL DU PORTRAIT
Acquisition du lexique
La constitution ensemble d'une carte mentale outil sur le portrait en fonction de ce qu'ils auront rencontré. L'objectif est d'étoffer leur vocabulaire de description et de trouver des synonymes au verbe être.
Télécharger « rédaction carte mentale portrait.pdf »
ETAPE 3: UNE PRODUCTION A LA MANIERE DE...
Un apprenti charpentier observe un vrai charpentier, reproduit ses gestes, s'entraine pour parvenir à la dextérité et l'habileté que demande ce métier. Un apprenti écrivain s'inspire de grands auteurs pour parvenir progressivement à une formulation bien tournée et intéressante. C'est ce que je propose à mes élèves.
Des trames de portraits" à la manière de" sont donc proposées pour guider le style des élèves et les aider à prendre modèle sur de grands auteurs...
3 JETS POUR SE PERFECTIONNER
En voyant la difficulté rédactionnelle de mes élèves, j'ai décidé de leur proposer quelque chose de très structuré pour qu'ils puissent apprendre à rédiger.
1 jet: sur la feuille ci-dessous aide à la formulation
Télécharger « CM le portrait fiche aide à la formulation élaborée par les élèves.pdf »

version "à la manière de " plus simple pour les CE2
Télécharger « portrait à la manière de ce2.pdf »
2ème jet : Ils reprennent la feuille d'aide à la formulation et récupèrent ce qu'ils ont écrit (1er jet) et le structure dans un texte écrit sur la feuille ci-dessous 2ème jet.
Télécharger « portrait rédaction étape 2 bis.pdf »

Entretien individuel avec la maitresse pour améliorer , structurer et corriger son portrait. Une correction écrite a été faite avec un code pour les répétitions, les erreurs orthographiques, les phrases mal dites...

3 ème jet: réécriture après correction avec les outils de la classe, dictionnaires, recherche de synonyme sur internet, tableau de conjugaison.... puis notation d'après les grilles de critères si-dessous.

ETAPE 4: EVALUER
Pour le 1er portrait + guidé en 3 jets (développé ci-dessus)
Télécharger « grille de critères portrait 1er »
Pour le 2ème portrait en 2 jets, plus libre. ils choisissent parmi les structures de phrases étudiées celles qu'ils souhaitent utiliser dans l'ordre de leur choix, à condition que cela respecte les codes d'un portrait. Puis ils viennent me voir en individuel après le 1er jet.
Télécharger « grille de critères portraits 2ème »
Voici des exemples de portraits particulièrement réussis. Les tournures étudiées et utilisées sont mises en gras.
Anouck cm1
La porte explosa, une adolescente vêtue d'un short et d'une veste bleu nuit pénétra dans la salle où je me trouvais. Elle était svelte plutôt jeune. De longs cheveux blonds encadraient un visage aux traits fins et aux yeux turquoise. Ils étaient d'un bleu profond et brillaient. Son court nez crochu donnait une impression étrange. Malgré la chaleur, elle n'enleva pas sa veste. Cette adolescente s'appelait Candice.
Gabriel cm2
La porte s'ouvrit et une jeune fille vêtue d'une robe noire pénétra dans la maison.
Elle semblait escogriffe, plutôt jeune. Des cheveux bruns en cascade encadraient un visage aux traits fins et aux yeux en amande. Elle dégageait une aura charmante à commencer par ses yeux noisette, parfait miroir de sa chevelure brune. Pourtant ceux qui la regardaient étaient frappés par son regard cruel.
Elle était très moderne avec son écharpe rose, sa robe noire et son manteau en cuir. Quelques touches personnelles agrémentaient cette tenue (...) : des boucles d'oreilles en or et un pendentif émeraude..
Cet accoutrement n'était toutefois pas assez original pour attirer véritablement le regard. Tout le monde n'y aurait plus pensé si, soudainement, elle n'était pas tombée.
Louise CM1
La porte s'ouvrit et une jeune fille apparut. Elle était vêtue d'un pantalon gris ardoise et d'un petit haut à rayures rose et bleu. Sa chevelure noire, parfait miroir de ses yeux sombres, étincelait. Son visage lisse et fin s'assortissait très bien avec son petit nez retroussé. Quand je la vis, je restai bouche bée comme certains autres avant moi. Elle avait une allure très étrange car, quand elle marchait, on aurait dit qu'elle volait. Quelques touches personnelles agrémentaient cette tenue dans le pur style anglais avec des boucles d'oreilles en or. Cette jeune fille s'appelait Oska.
Marie CM1
Cette dame se trouvait dans la forêt. Elle était vêtue d'une robe en peau de loup et de bottes noires aux motifs dorés. Autour de son cou se trouvait un pendentif. Ses yeux bleus étincelaient derrière quelques mèches de cheveux noirs; ces derniers étaient ondulés et très bien coiffés. Elle avait une vingtaine d'années et me regardait avec un regard touchant. Malgré la chaleur, elle ne portait pas d'habits adaptés à la chaleur. Cet accoutrement n'était toutefois pas suffisamment étrange pour que des personnes la remarquent.
Certains élèves se sont éloignés un peu plus des modèles proposés pour leur 2ème rédaction, tout en gardant certains verbes pour éviter les répétitions, le résultat est vraiment positif. Je vous mets quelques exemples.
Inès CM2
J'ouvris la porte du magasin et surgit cette femme aux yeux bleu ciel qui attirait l'attention. Elle était âgée d'une vingtaine d'années. Elle avait des cheveux blonds qui encadraient un visage fin. Elle dégageait beaucoup de bienveillance. Son petit nez fin, ses lèvres rouge framboise, la rendaient encore plus belle. Elle portait un tee-shirt noir qui ressortait bien avec son jeans violet et de petites chaussures à talon bas. Cette femme s'appelait Céline.
Loane CM2
Je me promenais au jardin public quand je remarquai cette femme. Elle portait une simple robe noire en parfait accord avec sa veste à paillette. Sa silhouette élancée lui donnait un air jeune; une magnifique chevelure brune encadrait un visage aux traits doux. Ses yeux en amande étincelaient. Sa démarche était féline et quand elle repoussa sa mèche devant son œil gauche, elle soupira longuement. Elle s'appelait Camille.
POUR ALLER + LOIN
Voici 2 portrait insérés dans un récit, l'objectif est de situer le contexte et de rendre son récit intéressant.
Pour aller plus loin... 3ème rédaction
Télécharger « à la manière de 3.jpg »
Télécharger « à la manière de 2.jpg »
 11 commentaires
11 commentaires
-
Je vous souhaite mes meilleurs vœux pour les fêtes de fin d'année...
Un petit cadeau, je vous partage mes toutes nouvelles cartes mentales
3 cartes mentales sur la division:
Une sur le passé simple
Si vous voulez les avoir en PDF, je vous invite à consulter la rubrique mes cartes d'organisation d'idées ICI
 3 commentaires
3 commentaires
-
Je viens de créer sur le blog une rubrique où je compte mettre mes nouvelles cartes mentales. Voici le lien ICI
 2 commentaires
2 commentaires
-
Je vous partage aujourd'hui mon travail sur "une nouveauté" des programmes que nous allons travailler demain avec les élèves. Si cela vous sert, la meilleure façon de me dire merci serait de me laisser un petit commentaire car j'y ai passé l'après-midi. :-)
Petite parenthèse car je tiens à m'insurger sur ce que j'entends un peu partout actuellement (primaires oblige) , les enseignants ne travaillent pas assez!!!! Comme si les heures devant élèves étaient les uniques heures que nous passions à travailler... J'en fais au moins le double en préparation/ corrections. Je n'ai jamais réellement fini, tant la masse de travail est conséquente. Mais pour le savoir, il faudrait que les personnes qui en parlent connaissent d'un peu plus près ce métier, Hé! Hé! Je ne leur donne pas une heure devant nos petits chérubins! Après j'adore ce que je fais mais j'aime nettement moins les préjugés sur notre profession très très loin de la réalité sur le terrain qui nous font passer pour des fainéants! Voilà c'est dit!
Petit retour de ma classe: mes élèves ont tous compris, cela leur a même donné envie d'écrire. Du coup demain, ce sont eux qui fabriqueront les phrases pour les exercices.
Bon voici les séances 1 et 2
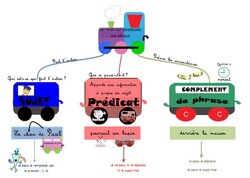
Je me suis servie de l'idée des wagons sur ce blog de Loustics ICI et de Jenny pour la locomotive ICI.
Télécharger « séquence les 3 groupes constituants de la phrase simple.pdf »
Télécharger « carte mentale constituants phrases.pdf »
Entrainement sur le net ICI
 votre commentaire
votre commentaire
-
Voici mes cartes mentales toutes nouvelles et toutes neuves!
Si vous ne connaissez pas le principe , je vous invite à regarder mes expérimentations sur la mémoire sur le blog.
En résumé, la carte mentale doit être l'aboutissement d'un travail de réflexion et de recherche des élèves. Elle est truffée d'indices de rappel visuels (pour retrouver dans ma mémoire à long terme où j'ai rangé les concepts étudiés) , de mots-clés hiérarchisés (indices de rappel phonologique ) .
Ma carte mentale est le résumé visuel et phonologique de ce qui a été dit et trouvé en classe. Elle est donc le produit fini qui n' a pour but qu'une réactivation rapide de ce qui a été mémorisé en classe. Ce sont en fait des cartes d'organisation d'idées. Plus c'est organisé, plus la mémoire aime ça!
Grammaire
Télécharger « carte mentale nom.pdf »
Télécharger « carte mentale verbe.pdf »
Télécharger « carte mentale constituants phrases.pdf »
Orthographe
Télécharger « fonction sujet carte mentale.pdf »
Télécharger « ortho eler eter.pdf »
Télécharger « ortho ger, cer.pdf »
Vocabulaire
Conjugaison
Télécharger « conjugaison 1 radical terminaison infinitif.pdf »
inspirée par ICI et là
Télécharger « carte mentale conjuguer un verbe leçon 2.pdf »
------------------------------------
 votre commentaire
votre commentaire
-
Pour récompenser la fidélité de certains de mes membres, j'ai créé une rubrique sous mot de passe qui leur sera réservée ICI .
Pour que je vous donne le mot de passe, il faut:
- être abonné à la newsletter
- avoir déjà mis plusieurs commentaires sur mon blog
- en faire la demande par mail en utilisant la même adresse mail que celle de la newsletter (pour vérification)
 4 commentaires
4 commentaires
-
Voici le lien vers mes expérimentations et réflexions sur la mémoire. Le chantier est vaste mais je commence à cerner peu à peu comment aider mes élèves dans ce domaine ICI
 2 commentaires
2 commentaires
-
Durant le 1er jour de rentrée, pour connaitre en profondeur mes élèves. Je leur fait passer ce test.
Mon projet sur la mémoire continue. Je me suis formée pendant les vacances pour comprendre en profondeur ce mécanisme complexe qu'est la mémorisation. Je vous en parlerai plus longuement lorsque les préparatifs de rentrée seront passés. ICI
Je fais remonter cet article (de l'année dernière) qui m'a permis de bien cerner le profil de mes élèves, pour les aider à diversifier leurs entrées. Plus il y a d'entrées variées (visuelles, auditives, kinesthésiques) plus la récupération des données mémorisées sera simple. Attention, un élève kinesthésique est un élève qui a la mémoire du mouvement.
ARTICLE DE L’ANNÉE DERNIERE
Je viens de lire l'excellent livre "apprendre autrement avec la pédagogie positive" que je vous recommande vivement.
Ce livre a très largement inspiré le travail qui suit (notamment les documents 1, 2, 3, 4).
Pour bien cerner le profil d'apprentissage de chacun de mes élèves, pour les aider à mieux apprendre, il est essentiel de comprendre le fonctionnement propre à chacun. Voici une activité qui devrait me faire gagner du temps dans ce domaine.
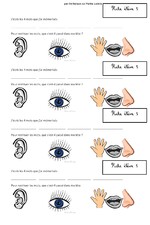
Dans les documents ci-dessous vous avez: la fiche enseignante, la fiche déroulement élève (à bien faire reformuler), 4 fiches élèves avec réponses proposées, une fiche résultat, un tableau pour noter le ou les profils de chaque élève (les numéros correspondent aux exercices proposés: 1= mot 1, 2= mot 2 etc).
DOC 1: Déroulement séance pour l’enseignant
DOC 2: Consignes pour les élèves.
DOC 3: l'enseignant dit le mot CHOCOLAT/ puis il l'écrit et l'efface ensuite. L'élève réfléchit à ce qui se passe dans sa tête et l'écrit sur la feuille ci-dessous..
DOC 4: l'enseignant dit le mot ENERGIE/ puis il l'écrit et l'efface ensuite. L'élève réfléchit à ce qui se passe dans sa tête et l'écrit sur la feuille ci-dessous.
DOC 5: l'enseignant dit le mot VACANCES/ puis il l'écrit et l'efface ensuite. L'élève réfléchit à ce qui se passe dans sa tête puis l'écrit sur la feuille ci-dessous.
DOC 6: l'enseignant dit le mot ECOLE / puis il l'écrit et l'efface ensuite. L'élève réfléchit à ce qui se passe dans sa tête puis répond sur la feuille ci-dessous.
Restitution des 4 mots mémorisés
DoC 6: Normalement, il y a une figure à reproduire que je n'ai pas mise car elle est directement tirée du livre. Il suffit de prendre une figure facile à reproduire avec des formes géométriques et quelques différences à droite et à gauche. Ensuite il faudra questionner l'élève sur sa façon de retenir la figure: il la voit dans sa tête, il se raconte comment elle est, il a passé avec son doigt le contour de cette figure.
DOC 7: L'élève peut maintenant prendre connaissance de son fonctionnement propre. Voici la fiche des résultats en fonction des réponses choisies. Une méthodologie pour bien retenir les cartes mentales construites en classe est alors proposée en fonction de chaque profil.
Voici le tableau permettant de visualiser les réponses et donc le profil dominant de chaque élève:
Et en version modifiable
Télécharger « fiche résultats.docx »
L'objectif sera aussi d'aider les élèves à varier leur palette évocative et pour cela, il est indispensable de "parler la langue d'apprentissage" de chaque élève.
--------------------------------------------
AJOUT nouveauté
Une seule fiche élève pour ceux qui sont restreints en photocopies .
 30 commentaires
30 commentaires
-
Au retour notre classe antiquité à Nîmes, les élèves ont :
- choisi leurs articles
- écrit plusieurs jets en les améliorant.
Une fois finis, nous avons choisi des titres en votant ainsi que le nom du journal.
Voici le résultat
Télécharger « journal p 1.pdf »
Télécharger « journal page 2.pdf »
Télécharger « journal p 3.pdf »
Télécharger « journal page 4.pdf »
 1 commentaire
1 commentaire
-
Lorsque Solène m'a contactée pour me demander d'écrire un article sur mon projet mémoire dans Beneylu Pssst, je me suis demandé si j'allais trouver suffisamment de matière pour le faire.
En faisant le bilan de tout ce que j'ai mis en place cette année, je me suis aperçue de toute l'avancée que j'avais faite dans ce domaine. Certes, le chemin qu'il me reste à parcourir est encore long, je ne suis qu'au début mais il est déjà prometteur... Je vais donc continuer dans cette lancée l'année prochaine...avec d'autres thèmes phares...
Mon article dans Beneylu Pssst ICI
Mon écrit intégral Télécharger « Comment aider ses élèves à mémoriser sur le long terme.pdf »
Points d'effort pour l'année prochaine:
- Des cartes mentales de mathématiques plus simples, une notion à la fois. Réactivation en un clin-d'oeil.
- Des exercices de relaxation plus fréquents, pour évacuer le stress et favoriser l'attention et la perception active.
- Des temps de mémorisation plus longs à l'école et avec encore plus d'entrées multiples.
- Un cahier de rituel avec pleins d'outils favorisant la réactivation de la mémoire (en conjugaison, grammaire, nombres, vocabulaire, mesures etc.) et faisant sens pour l'enfant. Objectif: une mémorisation de l'outil permettant de l'utiliser "mentalement" dans sa tête durant une évaluation.
TOUT UN PROGRAMME....
Un grand merci à Solène ...
 6 commentaires
6 commentaires
-
Avec les CM2 nous avons d'abord étudié et revu le futur simple de l'indicatif, sa construction et ses exceptions avant de faire cette séance... Ce qui est intéressant dans cette séance c'est la comparaison entre l'imparfait et le conditionnel présent. Exemple: courait= imparfait / courrait = conditionnel présent.
Dans le poème suivant (poème de Lucie un peu modifié) réalisé en rédaction (voir séance sur le genre poétique) souligne en bleu les verbes à l'imparfait et en rouge les verbes au conditionnel présent
Si Artémis était la biche
Si les arbres couraient dans le parc
Ils échapperaient aux flèches de mon arc.
Le Tartare se trouverait sur Terre
Hadès serait-il gentil
avec Artémis éblouie?
Si Héra se transformait en Zeus
Héphaïstos deviendrait-il peureux?
Si Cupidon devenait Hadès
L'amour rimerait avec tristesse
Si Aphrodite était hideuse
La beauté serait affreuse.
Nous serions tellement bien
Mais vous n'y comprendriez plus rien.
Maintenant que vous avez trouvé les verbes au conditionnel, pouvez-vous réfléchir à la façon dont ils sont construits.
Réactions des élèves: ça ressemble au futur au début mais les terminaisons ne sont pas celles du futur.
C'est le radical du futur et les terminaisons de l'imparfait.
A quoi sert ce temps+ mode? C'est un futur incertain (il faut certaines conditions pour que ça se passe).
- Si+ imparfait ===== le deuxième verbe sera au conditionnel présent.
- Formule de politesse (pourrais-tu...=
- Dans un récit au passé: Il était en train de lire car il savait que demain ce serait impossible pour lui.
Une fois qu'ils ont tout trouvé. On construit ensemble la carte mentale dont voici un exemple:
Télécharger « conjugaison-conditionnel-present.pdf »
Ils font les exercices de leur livre.
 2 commentaires
2 commentaires
-
Cette séance nous l'avons faite aujourd'hui et je suis super fière de mes élèves qui ont compris très vite et ont su réinvestir ce que nous avions déjà vu précédemment.
Révision de la valeur de chaque chiffre.
Nous avons revu la valeur de chaque unité x10, x100, x1000 avec l'aide d'un petit tableau surtout pour la partie décimale.
Télécharger « x par 10, 100 ou 1000.docx »
Ils sont arrivés à la conclusion que:
l'unité juste à gauche= 10 fois plus grande
2 rangs à gauche= 100 fois plus grande
3 rangs à gauche 1000 fois plus grande
Nous nous sommes entrainés avec toutes les valeurs: millièmes x10? x100? x1000? , dixièmes x 10? x100? ,centièmes, unités ....
Ils décalaient leur doigt sur le tableau puis dans l'espace devant eux.
Je leur ai donné 1 nombre 1, 005 qu'on a écrit en fraction (3 chiffres= millièmes= 1005/1000) puis la valeur de chaque chiffre 5 millièmes, 1 unité. X10
Les 5 millièmes x 10 deviennent 5 centièmes.
1 unité x10 deviennent 1 dizaine. Je mets la virgule entre les unités et les dixièmes. Cela fait donc 10,05
Je leur ai demandé de mettre dans le tableau chaque chiffre du nombre 1,005
- sur un jeton vert chaque chiffre de la partie entière
- sur un jeton rose, chaque chiffre de la partie décimale.
Avec leur voisin, ils fabriquaient le nombre 10 fois plus grand qu'ils plaçaient dessous. En changeant la couleur quand le chiffre passait dans la partie entière
1,005 x10 = 10, 05
Observez! Que s'est-il passé?
Réponses des élèves:
Elève 1: Les chiffres sont les mêmes mais la virgule a changé de place.
Elèves 2 et 3 : En fait, ce n'est pas la virgule qui a changé de place mais les chiffres car leur valeur a changé, ils se sont déplacés d'un rang vers la gauche (valeur 10 fois plus grande) . Du coup la virgule reste toujours entre les unités et les dixièmes qui sont décalés d'un rang vers la droite par rapport au nombre de départ .
On gestue tout ça.
Quelle règle? Lorsque je multiplie un nombre décimal par 10, la virgule sera décalée d'un rang vers la droite...par rapport au nombre de départ car la valeur des chiffres a changé. La virgule reste entre les unités et les dixièmes. Les unités et les dixièmes ont bougé.
On essaie avec d'autres nombres: 12,02x10= / 4,025x10 ...
Ils voient que la règle qu'ils ont trouvé marche.
Et pour x100? Les élèves ont trouvé tout de suite. C'est pareil mais sauf que c'est 2 rangs.
Et pour x1000? C'est pareil sauf que c'est 3 rangs.
Nous en arrivons à la carte mentale
Télécharger « CARTE MENTALE X D2CIMAUX.pdf »
Carte complétée:
Télécharger « carte mentale x 10, 100 ... d'un décimal.pdf »
 votre commentaire
votre commentaire
-
Nous avons travaillé sur les codes du poème puis nous avons analysé 3 poèmes. certains se sont inspirés de leurs structures pour construire leur propre poème.
Télécharger « poèmes mythologiques modèle.pdf »
Voici un échantillon de poèmes réalisés par les enfants.
Poème de Lucie C (CM2)
Si Artémis était la biche
Si la biche devenait les flèches
Si les arbres couraient dans le parc
Ils échapperaient aux flèches de mon arc
Le Tartare se trouverait sur Terre
Hadès serait-il gentil
Avec Artémis éblouie?
Si Héra se transformait en Zeus
Héphaïstos serait-il peureux?
Si Cupidon devenait Hadès
L'amour serait tristesse
Si Aphrodite était hideuse
La beauté serait affreuse
Si Pégase marchait comme Cerbère
Mais le monde serait à l'envers.
--------------------
Poème de Noé (CM2)
Si j'étais Dieu, je serais celui de la glace
J'aurais le pouvoir d'un trou noir de l'espace
J'habiterais une maison gelée
Si j'étais Dieu
Si j'étais Dieu, personne ne viendrait me visiter
Je pourrais te congeler
Si tu voulais m'embêter
Si j'étais Dieu.
Si j'étais Dieu, je serais le plus puissant
J'aurais le respect de tous les dieux
Je tuerais tous les méchants
Si j'étais Dieu.
Je serais autant talentueux
que majestueux,
Les hommes pourraient être hideux,
Affectueux ou généreux,
Ils seraient tous sous l'autorité
de ma grande divinité.
Si j'étais Dieu.
----------------------
Poème de Marie (CM2)
Si Pégase n'était pas ailé
si Héra n'était pas une calamité
Si Zeus n'avait pas d'éclair
Si Hermès n'aimait pas être en l'air.
Si Apollon n'était plus le plus beau
Si Artémis ne protégeait plus les animaux
Si Dionysos n'aimait plus le vin
Si Poséidon n'avait pas le pied marin.
Si Arès ne combattait plus
Si Aphrodite ne posait plus nue
Si Athéna avait perdu la raison
Si Déméter n'aimait plus la moisson,
Les dieux seraient tellement tristes de ne pas avoir de pouvoir.
Quel ennui ce monde à l'envers
L'Olympe ne serait plus qu'une misère.
----------------------------
Poème de Lou-Anne (CM2)
Si j'étais déesse de la musique
Je chanterais avec passion
Pour provoquer un déclic
Une grande émotion
En chantant je mettrais du baume au coeur
Et fini les pleurs, plus que du bonheur
Plus d'Hadès
Fini la tristesse
Ce n'est pas la réalité
Mais c'est bien de rêver
En toute liberté
et sans se faire critiquer.
Poème de Maëlle (Cm2)
Si j'étais une déesse
Je serais Aphrodite
De tous les dieux
Je serais la favorite
Dans mon coeur
Il n'y aurait que de la fraicheur
Je sèmerais du bonheur
Avec beaucoup d'ardeur
Et de splendeur
Tous les gens m'aimeraient
et tout le monde m'admirerait
Mais hélas ce n'est pas la réalité
Je suis en train de rêver.
---------------------
Poème de Benjamin B (CM1)
Si j'étais une déesse
Ma passion serait tendresse
J'aurais été la fille d'Hermès
Plein de gentillesse
J'irais à Beauty Succès
Mais si j'étais une déesse
On pleurerait de tristesse.
----------------------
Poème de Kévin (CM2)
Si j'étais un dieu de la mythologie
La flamme serait mon amie
Les gens ne feraient plus la guerre
de Zeus, je serai le troisième frère.
Que de l'amour sur la Terre
Plus de misère, ni de colère
Il n'y aurait plus de peur
dans nos coeurs
Plus de gens qui pleurent
mais du bonheur
Mais je rêve, je ne suis qu'un simple mortel
pas éternel.
-----------------
Poème de Pierre (CM1)
Si Paris était l'Olympe
Si Hadès était une princesse
Si le minotaure était un porc
Si Cerbère faisait la taille de la Terre
Si Poséidon n'était pas le dieu poisson
Si Hercule était nul
Si Pégase avait des gaz
Mais tout cela n'existe pas ...et pourquoi pas?
-------------------
Poème de Lucie de J.
Quelle drôle de mythologie!
Si dans l'Olympe, Athéna
Se mettait à faire des plats
Les dieux ne seraient plus au ciel
Si toutes les Bénédictes
Devenaient des Aphrodites
Elles seraient tellement belles.
Si dans l'Olympe tous les dieux
Devenaient paresseux
Hadès en profiterait
Pour pouvoir déchainer
Toutes ses haines et ses fureurs
Et surtout tous ses malheurs
Sans exception, tous les saints
Pour lui seraient des pantins
Ce monde serait tellement bien
Mais on n'y comprendrait plus rien.
 6 commentaires
6 commentaires
-
Je participe à un rallye-liens proposé par Delfynus sur ces projets qui recoupent plusieurs matières . Pour voir les autres projets cliquez sur l'image si-dessous
Voici mon projet sur le thème de la mythologie
VOICI NOTRE DÉBUT DE PROJET
Organigramme prévisionnel
Petite erreur dans "mes séances de rédaction" ce n'est pas Hercule mais Ulysse qui rencontre un cyclope. Je corrigerai dès que possible.
- Séance 1: qu'est-ce qu'un mythe + les dieux grecs ICI
RITUEL
- Hercule a besoin de l'aide de la classe pour l'aider dans ses épreuves.Rituels sur les 12 travaux d'Hercule avec un défi à la classe pour chaque épreuve. ICI
Casse tête géométrique, problèmes amazoniens, orientation dans le Tartare, charades sur les créatures mythologiques, acrostiche mytho, luttes contre les cavales, art visuel pour distraire le lion de Némée, orthographe pour avoir les indices de la Pythie de Delphes, les épreuves et les indices seront multiples... un bon moyen de se creuser les méninges de bon matin. (Pour voir les corrigés, il faut aller sur le blog classe).

- Séquences de rédaction
1) Type descriptif dans un récit narratif: Raconte-moi ta créature hybride ICI
2) Type poétique écrire un poème sur le thème de la mythologie ICI
-----------------------------------------------------------
En résumé, nous avons travaillé la mythologie:
- en anglais (littérature anglaise sur des classiques comme Hercule, Ulysse)
- en art visuel, ils ont dessiné leurs créatures hybrides puis ont fabriqué leur déguisement en respectant leur portrait+ travail sur la sculpture antique.
- en sport : expression corporelle (projet spectacle= gestuelle des dieux, défilé des créatures) + olympiades inter-écoles (explication des jeux olympiques)
- en français grâce aux projets rallye-lecture, travail en rimes sur les dieux (spectacle) et rédactions (description, poème) + vocabulaire les expressions mythologique= talon d’Achille, faire sa Cassandre etc., mots d'origine gréco-latine ...
- en informatique, ils ont cherché des précisions sur leur dieu pour pouvoir créer un texte dessus (pour le spectacle), des rimes aussi. Ils ont tapé leurs poèmes et leurs portraits dans un logiciel de traitement de texte.
-en histoire des arts du cinéma avec le film de Percy Jackson
Télécharger « histoire des arts du cinéma.pdf »
- en histoire des arts visuels avec les dieux à dessiner comme les statues antiques + classe verte (à la rentrée) à Nimes + Toulouse etc.
- en maths sur le vocabulaire en langue latine : deci, milli, et en grec ancien : hecto, kilo,polygone et les noms des polyèdres, la lettre Pi empruntée à l'alphabet grec... Nous avons vu les jours de la semaine en l'honneur des dieux romains (vus dans les 12 travaux d'Hercule version romaine). puis un peu d'astronomie en sciences avec les planètes...
---------------------------------------------------
PROJET SPECTACLE: Avec l'aide d'une spécialiste en mise en place du corps Gabrielle, la classe a monté un spectacle d'une vingtaine de minutes sur la mythologie.
Les élèves ont tout créé: l'histoire, les costumes de monstres pour le défilé de monstres (lorsque Baptiste dessine) les habits des dieux de l'Olympe, du minotaure, le livre magique, les chorégraphies en lien avec leurs dieux et les voix de la chanson de la fin. Les 3 élèves qui faisaient Hermès ont souhaité arriver sur scène en skate. Nous avons fait le spectacle hier et ils ont tous été géniaux.
Voici les bandes sons mais ils ont été bien mieux en direct sur scène. Nous avions travaillé la mise en voix, si bien qu'ils ont pu dire le texte fort sans micro et que tout le monde a très bien entendu..
Ces versions mp3 ne sont que le pâle reflet de ce qu'ils ont fait, les bandes musicales sont raccourcies et vous ne voyez pas le jeu scénique...mais ça donne une idée de la richesse de ce projet!
Voici notre livre magique entièrement fabriqué par les élèves .
Partie 1: le livre magique
Partie 2: le monde des dieux
REMARQUES sur le spectacle:
1) La partie narrative n'est pas faite par le même élève que la partie dialoguée alors qu'il s'agit du même personnage. L'explication est simple, le texte narratif était dur à mémoriser nous l'avions donc enregistré en voix off avec une autre élève très forte pour cet exercice..
2) Le labyrinthe était constitué des élèves tenant chacun un grand carton (3 rangées) avec un visuel garanti surtout lorsqu'ils se poussent dans les coulisses pour laisser apparaitre le minotaure.
3) Lorsque Baptiste (le héros) enlève son empreinte du livre (partie 1) il y a une partie percussions corporelles où les élèves placés derrière lui reproduisaient chaque rythme en écho.
4) Lorsqu'il dessine les créatures, les élèves défilent un par un dans le costume de la créature qu'ils ont fabriquée en tenant compte de leur portrait de créature hybride (travail en rédaction)
5) Excepté les Hermès qui arrivent en skate, chaque apparition de dieu se fait sur de la musique avec une chorégraphie créée par les élèves en lien avec la personnalité des différents dieux.
6) Pour la cup song, les dieux observent Baptiste puis tout l'olympe la fait . Elle est chantée par 2 élèves de la classe.
VERSION ECRITE (il y a certainement des coquilles )
Télécharger « pièce de théâtre mythologique.pdf »

Liens vers d'autres blogs et d'autres exploitations de ce thème
Je complète par le magnifique rallye lecture de Bout de Gomme ICI
L'histoire des Arts chez classeur école en lien avec la mythologie ICI
et les dictées d'Histoire des Arts d'Orphée ICI
Voici de belles idées chez Craie Hâtive ICI
 8 commentaires
8 commentaires
-
Je me permets de réagir par cet article, suite à la succession d'articles et de mails contre cette réforme d'orthographe...
On parle de "nouvelle "réforme alors qu'elle date de 26 ans. Elle n'est donc pas nouvelle. On l'applique depuis un moment déjà dans les classes car cela nous est demandé dans les anciens programmes. Alors pourquoi ces réactions tardives?
On entend que l'accent circonflexe va être supprimé totalement, encore une fois, c'est faux.
Nénuphar est devenu nénufar comme avant 1935...Un retour aux origines en somme.
En bref tout a une explication et je fais confiance à ceux dont c'est le métier, qui connaissent la langue sur le bout des doigts pour la faire évoluer intelligemment... et c'est ce qu'ils font!
Voici un lien vers la fausse rumeur de disparition de l'accent circonflexe ICI
Je vous partage le magnifique article de Charivari qui développe fort bien le contenu de cette réforme. (Cliquez sur l'image)
 4 commentaires
4 commentaires
"Enseigner, c'est influencer une vie pour toujours"